Fiziko - baza kurso/Kelkaj bazaj grandoj

Ĉapitroj

Forto

Por la forto estas uzata la formula simbolo F .
Fortoj estas ekkoneblaj nur pro iliaj efikoj.Tiuj estas aŭ akcelo aŭ deformo.
Forto kaŭzas akcelon de libera korpo (dinamika efiko)
Forto kaŭzas deformiĝon de fiksata korpo (statika efiko)
Ĉiam, kiam korpo ŝanĝas sian rapidon aŭ deformiĝas, tio okazas, ĉar iu forto efikas al ĝi.

Mezuro de forto

Fortomezuriloj enhavas ŝtalajn risortojn, kiuj plilongiĝas proporcie al la forto.

Mezuro signifas komparo. Por mezuri fortojn bezonas kompari ĝian efikon kun la efiko de la mezurunuo. Tio estas pli facila por la statika efiko.
Du fortoj estas egalgrandaj, kiam ĝi deformas saman korpon egalgrade!
Kiel deforminda korpo kutime estas uzata stala risorto.
La mezurunuo de la forto estas la neŭtono. [F] = 1 N (neŭtono)
La neŭtono estis tiel nomita omaĝe al la brita fizikisto Isaac Newton.^[1]
Neŭtono ne estas baza unuo de la SI-sistemo. Pro tio kompleta difino de neŭtono estas Tiu rilato estos klarigata en ĉapitro Por ĉi ĉapitro ni uzas la sekvan difinon:
1 N estas la forto, kiu plilongigas norman risorton je difinita distanco.

Fortomezuriloj enhavas tiujn normajn risortojn.

Forto kiel vektoro

La efiko de forto dependas ne nur de ĝia intenseco sed ankaŭ de ĝia direkto.
Pro tio fortoj estas reprezentataj pere de sagoj (vektoroj). La longo de la sago estas mezuro de la intenseco, kaj la pinto montras la direkton.
Por ĝuste reprezenti fortojn, necesas difini fortoskalon. Ekzemple 5 N ∞ 2,5 cm signifas, ke la sago, kiu reprezentas forton de 5N, devas esti longa 2,5cm.
Kiam necesas, klare indiki, ke la forto estas vektora grando, oni skribas ĝin kun sago super la formula simbolo

Leĝoj de Newton pri movo

La tri leĝoj de Newton pri movo estas sciencaj leĝoj pri konduto de movitaj korpoj. Ili estas fundamentaj en klasika mekaniko.

La unua leĝo - leĝo de inercio

Korpo restas senmova, aŭ en uniforma movostato, krom se agantaj fortoj devigas ĝin ŝanĝi sian staton.
Do korpo restas sen movo, aŭ en uniforma movostato, se ne agas forto sur ĝin, aŭ, se la vektora sumo de ĉiuj fortoj agantaj estas nulo.

Kiam la forto puŝanta F_P kaj la forto frotanta F_F havas saman intensecon, la kesto moviĝas uniforme

Ekzemple, la kesto en la figuro moviĝas unuforme, kiam la forto puŝanta F_P kaj la forto frotanta F_F , havas saman intensecon. En ĉi tiu kazo, ĉar ili havas kontraŭan direkton,la vektora sumo estas nulo.

La dua leĝo – leĝo de agado

La ŝanĝo de movostato de korpo estas proporcia al la forto aganta kaj havas la saman rektlinean direkton kiel la forto.
Nuntempe, anstataŭ ŝanĝo de movostato, estas kutime uzata la vorto akcelo (formula simbolo a). Tiam la dua leĝo iĝas:

Akcelo de korpo estas proporcia al la forto aganta kaj havas saman rektilinian direkton kiel la forto.

La leĝo povas esti skribita kiel formulo a ≈ F
Surbaze de ĉi tiu leĝo Leonhard Euler en la jaro 1750 unue formulis la bazan leĝon de la dinamiko F = m⋅a

La tria leĝo - leĝo de reciproka agado

A agas al B kun la sama forto kiel B al A

Kiam iu ajn korpo A efikas per forto sur alian korpon B, la dua korpo B efikas per egala kaj kontraŭa forto sur la unuan korpon A.

Alia formulado estas ke, kiam ekzistas forto, aganta sur korpon A, kaŭze de alia korpo B, ekzistas ankaŭ reciproka forto, aganta sur korpon B kaŭze de korpo A.

Tiuj ĉi formuladoj implicas ke se iu agas sur korpon kun forto F_AB, tiam ankaŭ la korpo agas sur tiun kun forto F_BA = -F_AB. La reago-forto havas la kontraŭan direkton de la ago-forto kaj saman intensecon.

Forto kaj etendo - leĝo de Hooke

Eksperimento 1.1 - Rilato inter forto kaj etendo por ŝtala risorto

Ni etendas risorton mezurante kaj la forton kaj la rezultantan etendon, kiel montras la figuro.
Ni trovas la valorojn de la sekva tabelo. Kun tiuj valoroj povas esti desegnata la diagramo de la figuro.

MP	s[mm]	F[N]
1	16,0	0,5
2	33,0	1,0
3	50,0	1,5
4	67,0	2,0
5	86,0	2,5
6	103,0	3,0

El diagramo rezultas, ke rekto trairante la originon de la koordinatsistemo bone aproksimiĝas al la valoroj de la ses mezurpunktoj. Tio signifas, ke la fortoj etendantaj kaj la etendoj por ŝtala risorto estas proporciaj.

Risortkonstanto

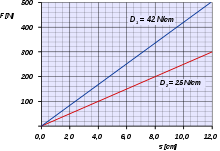
La konstanto trovata en eksperimento 1.1, estas karakteriza valoro por ĉiu unuopa risorto. Ĝi nomiĝas risortkonstanto kaj oni uzas formulan simbolon D por ĝi. Ju pli malmola estas la risorto, des pli granda estas D kaj des pli apika estas la rekto en la s-F diagramo.

$D={\frac {F}{s}}\to [D]={\frac {1N}{1m}}=1{\frac {N}{m}}$

Ĝenerale, ĉiu sistemo, por kiu la etendo estas proporcia al la forto etendanta, obeas al la leĝo de Hooke.^[2] Alivorte, kiam iu sistemo obeas al la leĝo de Hooke, ĝia etendo estas proporcia al la forto etendanta.

Ekzemplo

La risortaro de la teknika aranĝaĵo de montrita en la figuro estas faita el du risortoj kun risortkonstantoj

La risorto 1 staras interne de la risorto 2; sen ŝarĝo ili havas la saman longon.

a) Je kiom da centimetroj la risortaro estas kunpremita, kiam ĝi estas ŝarĝata kuntuta forto egala al 500 N

b) Kiom grandas la risortkonstanto de la tuta risortaro?

Solvo
a)

 $F=F_{1}+F_{2}=D_{1}\cdot s+D_{2}\cdot s=s\cdot (D_{1}+D_{2})$ 


 $s={\frac {F}{(D_{1}+D_{2})}}={\frac {500N}{(42{\frac {N}{cm}}+25{\frac {N}{cm}})}}=7,46{cm}$

b)

  $D={\frac {F}{s}}=D_{1}+D_{2}=67{\frac {N}{cm}}$

Respondo

La risortaro estas kunpremita je 7,46 cm, kaj ĝia risortkonstanto egalas 67 N/cm.

Kompensolinio - kompensorekto

Kompensolinio nomiĝas la geometria linio, kiu plej bone proksimiĝas al la mezurpunktoj en diagramo ^[3] En kazo de la eksperimento priskribita supre, tiu linio estas rekto, nome la kompensorekto.

Rigardante la poziciojn de la mezurpunktoj en la diagramo rezultanta el la mezurpunktoj, oni vidas, ke neniu de la punktoj 1-6 troviĝas precize sur la rekto. Fakte, kalkulante la risortkonstanton, la rezultoj estas malsamaj por la diversaj punktoj.

Ekzemple:

Mezurpunkto MP2: $F_{2}=1{,}0N\quad s_{2}=33mm\to D_{2}={\frac {1{,}0N}{0{,}033m}}=3{,}0{\frac {N}{m}}$
Mezurpunkto MP6: $F_{6}=3{,}0N\quad s_{6}=103mm\to D_{6}={\frac {3{,}0N}{0{,}103m}}=2{,}9{\frac {N}{m}}$

Kiu estas la ĝusta valoro de D por la risorto eksamenita en la eksperimento?

La plej bona valoro estas tiu, kiu rezultas el iu punkto, kiu troviĝas sur la kompensorekto.

Unu el tiaj punktoj estas la punkto P markita en la figuro.

Por la punkto P rezultas: $F=2{,}3N\quad s=78mm\to D={\frac {2{,}3N}{0{,}078m}}=2{,}9{\frac {N}{m}}$

Do la plej bona valoro rezultante el la mezursekvenco de la eksperimento estas D = 2,9 N/m.

Maso

Kopio de la prakilogramo protektita per du vitraj kloŝoj

Por la maso estas uzata la formula simbolo m .

La maso estas baza fizika grando, ĝi estas eco de korpoj.

La maso de iu korpo restas la sama, kie ajn ĝi estas en la universo.

Mezuro de la maso

La mezurunuo de la maso estas la kilogramo 1 kg

Ekde 1889 unu kilogramo egalas, laŭdifine, al la maso de la "prakilogramo", metala cilindro el aparta alojo de plateno (90% de la maso) kaj iridio (10%), kies oficiala nomo estas Pt‑10Ir. La specimeno estas konservata en la Oficejo Internacia pri Pezoj kaj Mezuroj, en Sèvres apud Parizo. Tiun prototipon oni uzas por kompare kontroli la masojn de ĝiaj kopioj, kiujn ricevis landoj uzantaj la metran sistemon.

Por mezuri la mason estas uzata pesilo, ekzemple vektopesilo aŭ risortopesilo.

Efektive, pesiloj ne mezuras la mason, sed ili komparas nur la pezoforton, kiu agas sur la mezurenda maso kun tiu, kiu agas sur la mezurunuo t.e. la mezurpeziloj. Sed la pezoforto dependas de la loko, en kiu la korpo troviĝas. Pro tio tre gravas, ke la mezurunuo kaj la mezurenda maso estas komparataj en la sama loko.

Kompreneble, kiam oni uzas vektopesilon, la mezurenda maso kaj la mezurpeziloj ĉiam troviĝas en sama loko.

Kiam oni uzas risortopesilon, la valoro indikata estas preciza nur en la loko, kie la pesilo estis laŭnormigita.

Pezoforto

Masoj altiras unu la alian.^[4] La pezoforto ( formula simbolo $F_{G}$ ) estas la forto, kun kiu la tero altiras korpojn, kiuj staras sur ĝi. Tiu forto estas nomata ankaŭ gravitoforto.^[5] La pezoforto ne estas konstanta. Ĉar ĝi estas interago, inter la tero kaj la korpo, ĝia intenso ŝanĝiĝas kun la pozicio sur la tero. La diferenco inter la pezofortoj, kiuj agas sur la saman korpon en diversaj lokoj de la tero, estas malgranda, sed bone mezurebla.

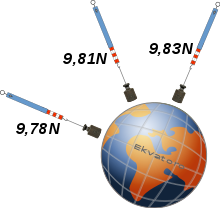
Por maso egala al m=1kg rezultas:

sur norda poluso $\qquad \quad F_{G}=9{,}83N$

sur la 45a latitudo $\qquad \quad F_{G}=9{,}81N$

sur ekvatoro (marnivelo) $\qquad F_{G}=9{,}78N$

en Chimborazo Ekuadoro je la altitudo de 6000m $\quad F_{G}=9{,}77N$

Averaĝe, sur la tero, maso egala al 1kg estas altirata kun pezoforto de 9,81N . Oni diras, ke sur la tero la lokofaktoro aŭ gravita akcelo(^[6] egalas 9,81 N/kg. La formula simbolo de tiu faktoro estas g.

Kelkaj valoroj de g :

Tero    9,81 N/kg      Luno       1,62 N/kg
Marso   3,70 N/kg      Jupitero  23,12 N/kg

Ĝenerale validas: pezoforto = maso x lokofaktoro $\qquad \quad F_{G}=m\cdot g$

Ekzemplo

Al risorto kun risortkonstanto D = 25 N/m estas pendigata maso de 200 g .

a) Je kiom da centimetroj la risorto estos plilongigata?

b) Kiom estus plilongigata la risorto sur la Luno?

Solvo

$D=25{\frac {N}{m}}\qquad m=200g$

$sur\;la\;tero:g_{T}=9{,}81{\frac {N}{kg}}$ $\qquad sur\;la\;luno:g_{L}=1{,}62{\frac {N}{kg}}$

a) $sur\;la\;tero:F_{T}=m\cdot g_{T}=0{,}20{kg}\cdot 9{,}81{\frac {N}{kg}}=1{,}96{N}\ \ \ \ \ s_{T}={\frac {F_{T}}{D}}={\frac {1{,}96{N}}{25{\frac {N}{m}}}}=0{,}0784{m}=7{,}84cm$

b) $sur\;la\;luno:F_{L}=m\cdot g_{L}=0{,}20{kg}\cdot 1{,}62{\frac {N}{kg}}=0{,}32{N}\ \ \ \ \ s_{L}={\frac {F_{L}}{D}}={\frac {0{,}32{N}}{25{\frac {N}{m}}}}=0{,}0128{m}=1{,}28cm$

Rezulto: Sur la Tero la plilongigo egalas 7,8 cm kaj sur la Luno 1,3 cm.

Solvendaj problemoj

1. La maldekstra bildo montras suspension de aŭtomobilo kun ĝia risorto. La risortkonstanto egalas 16 N/mm. En la aŭto sidiĝas kvar personoj kun totala maso de 300 kg. La tuta pezo dispartiĝas egale sur la kvar radoj. Je kioma distanco ĉiu risorto estas kunpremata?

2. Du risortoj, kun risortkonstantoj D1 = 4,2 N/cm kaj D2 = 2,5 N/cm, estas pendigitaj unu al la alia. Kiam al la du risortoj estas pendigata fera sfero, ili estas plilongigataj entute je 25 cm. (vidu bildon dekstre)

a) Kalkulu la mason de la sfero !

b) Kiom grandas la tuta risortkonstanto de la grupo de du risortoj?

Denso

Por la denso estas uzata la formula simbolo $\rho$ (greka rho).

La denso aŭ volumena maso estas karakteriza eco de materialoj.

Eksperimento- Rilato inter maso kaj volumeno de korpoj el sama materialo

La korpoj en la bildo, estas ĉiuj faritaj el sama materialo, aluminio. Determinante volumenon ^[7] kaj mason de la korpoj, oni trovas la valorojn de la sekva tabelo.

MP	V[cm³]	m[g]
1	7,6	20,3
2	11,5	32,2
3	16,5	44,5
4	28,7	80,2

Kun tiuj valoroj povas esti desegnata la apuda diagramo.

El la diagramo rezultas, ke rekto trairante la originon de la koordinatsistemo bone proksimiĝas al la valoroj de la mezurpunktoj.

Tio signifas, ke maso kaj volumeno por korpoj el sama materialo estas proporciaj. $\qquad {\boldsymbol {m\propto V\rightarrow {\frac {m}{V}}=konst}}\quad$ por korpoj el la sama materialo.

Denso

La konstanto eltrovita en la supra mezurserio estas karakteriza valoro por ĉiu materialo. Ĝi nomiĝas denso aŭ volumena maso kaj oni uzas formulan simbolon ρ (greka rho) por ĝi.

{\boldsymbol {\rho ={\frac {m}{V}}\qquad \left[\rho \right]={\frac {1kg}{1m^{3}}}=1{\frac {kg}{m^{3}}}}}

Por aluminio rezultas el la punkto P de la kompensorekto de la diagramo: $\quad V=22cm^{3}\quad m=60g\quad \rightarrow \quad \rho ={\frac {m}{V}}={\frac {60g}{22cm^{3}}}=2,7{\frac {g}{cm^{3}}}=2700{\frac {kg}{m^{3}}}$

Uzante la mezurunuon kg/m³, solidaj korpoj havas relative grandan denson. Pro tio kelkfoje oni preferas uzi aliajn unuojn kiel g/cm³ aŭ kg/dm³.

{\boldsymbol {1000{\frac {kg}{m^{3}}}=1{\frac {g}{cm^{3}}}=1{\frac {kg}{dm^{3}}}}}

Ĉi sekve troviĝas tabelo kun ekzemploj por la denso de kelkaj kemiaj elementoj kaj aliaj substancoj.

elementoj ĉe 20°C	denso [kg/m³]	substancoj solidaj	denso [kg/m³	substancoj likvaj kaj gasaj**	denso [kg/m³
plateno	21450	diamanto	3520	mara akvo	1030
oro	19320	granito	~ 2800	pura akvo (4 °C)	1000
hidrargo*	13550	marmoro	~ 2800	etanolo	790
plumbo	11340	vitro	~ 2600	benzino	700
arĝento	10490	sablo	~ 1500	butano	2,73
kupro	8950	akrilvitro	1200	aero	1,29
nikelo	8900	glacio (0°C)	920	metano	0,72
fero	7860	ligno	400-800	helio	0,18
aluminio	2700	korko	200-400	hidrogeno	0,09
*likva				**ĉe 0°C kaj 1013 hPa

Ekzemplo 2.3

Sfero estas farita el fero kaj havas diametron je 7,5 cm. Kalkulu la mason de la sfero!

Solvo

d=7{,}5cm\quad \rho =7{,}86{\frac {g}{cm^{3}}}\qquad \rightarrow \quad V={\frac {d^{3}\cdot \pi }{6}}={\frac {{{7{,}5cm}^{3}}\cdot \pi }{6}}=221cm^{3}

\rho ={\frac {m}{V}}\quad \rightarrow \quad m=v\cdot \rho =221cm^{3}\cdot 7{,}86{\frac {g}{cm^{3}}}1737g=1{,}74kg

Rezulto: La maso de la sfero sumiĝas je 1,74 kg.

Ekzemplo 2.4

La prakilogramo estas cilindro kun diametro egala al 39 mm. La alojo, el kiu ĝi estas farita, havas denson de 21550 kg/m³. Je kiom egalas ĝia alto?

Solvo

m=1kg\quad \rho =21{,}55{\frac {g}{cm^{3}}}\qquad d=3{,}9cm\qquad A=\left({\frac {d}{2}}\right)^{2}\cdot \pi =\left({\frac {3{,}9cm}{2}}\right)^{2}\cdot \pi =11{,}95cm^{2}

\rho ={\frac {m}{V}}\quad \rightarrow \quad V={\frac {m}{\rho }}={\frac {1000g}{21{,}55{\frac {g}{cm^{3}}}}}=46{,}4cm^{3}\qquad V=A\cdot h\quad \rightarrow \quad h={\frac {V}{A}}={\frac {46{,}6cm^{3}}{11{,}95{cm^{2}}}}=3,88cm

Rezulto: La alto de la cilindro egalas al 3,88 cm.

Solvendaj problemoj

Sfero farita el fero, kun diametro de 8,6 cm estas pendigita al risorto, kiu havas risortkonstanton egala je 12 N/cm.
Je kiom la longo de la risorto pliiĝas?
ingoto el oro
Sur la du pesiltasoj de vektopesilo troviĝas du egalaj glasoj. La unua enhavas 80 cm³ da etanolo, la dua enhavas akvon.
Kiom da akvo (en cm³) troviĝas en la dua glaso, kiam la pesilo estas en ekvilibro?
Sfero farita el fero, kun diametro de 8,6 cm estas pendigita al risorto, kiu havas risortkonstanton egala je 12 N/cm.
Je kiom la longo de la risorto pliiĝas?
Klasĉambro longas 9,30 m, larĝas 8,2m kaj altas je 3,5 m.
Kalkulu la mason de la aero enhavita en la ĉambro!
La dekstra bildo montras ingoton el oro kun maso de 1 kg.
Kalkulu ilian volumenon!

Respondoj al la solvendaj problemoj de la ĉapitro

Problemoj el paragrafo 2

Ĉiu risorto estas kunpremata je 4,6cm.
a) La maso de la sfero egalas 3,99 kg
b) La risortkonstanto de la grupo de du risortoj egalas 1,57 N/cm.

Problemoj el paragrafo 3

La risorto plilongiĝas je 2,14 cm.
En la dua glaso troviĝas 63,2 cm³ da akvo.
La maso de la aero en la ĉambro egalas 344 kg.
La volumeno de ingoto egalas 51,8 cm³.

Referencoj

↑ Isaac Newton https://eo.wikipedia.org/wiki/Isaac_Newton
↑ Leĝo de Hooke https://eo.wikipedia.org/wiki/Leĝo_de_Hooke
↑ En statistiko tiu linio nomiĝas regresa kurbo kaj ekzistas metodoj por precize kalkuli ĝin. Ĝi estas facile trovebla ankaŭ uzante tabelkalkulprogramon de komputilo.
↑ Pro gravito ĉiuj mashavaj objektoj altiras unu la alian reciproke. La intenso de la rezultanta forto dependas de la distanco inter la masoj kaj ilia valoro.
↑ En la ĉiutaga parolado la maso estas kutime nomata pezo. En fiziko tio estas nerekomenda, ĉar tiamaniere estus faciligata konfuzo inter maso kaj pezoforto
↑ [[1]]
↑ Por trovi precizan valoron de la volumeno ni uzas la metodon de Arkimedo, enakvigante la korpojn. La metodo estos klarigata en alia ĉapitro

[1] Isaac Newton https://eo.wikipedia.org/wiki/Isaac_Newton

[2] Leĝo de Hooke https://eo.wikipedia.org/wiki/Leĝo_de_Hooke

[3] En statistiko tiu linio nomiĝas regresa kurbo kaj ekzistas metodoj por precize kalkuli ĝin. Ĝi estas facile trovebla ankaŭ uzante tabelkalkulprogramon de komputilo.

[4] Pro gravito ĉiuj mashavaj objektoj altiras unu la alian reciproke. La intenso de la rezultanta forto dependas de la distanco inter la masoj kaj ilia valoro.

[5] En la ĉiutaga parolado la maso estas kutime nomata pezo. En fiziko tio estas nerekomenda, ĉar tiamaniere estus faciligata konfuzo inter maso kaj pezoforto

[6] [[1]]

[7] Por trovi precizan valoron de la volumeno ni uzas la metodon de Arkimedo, enakvigante la korpojn. La metodo estos klarigata en alia ĉapitro

[1]

[2]

[3]

[4]

[5]

[6]

[7]